Maps and Hashing

John Mieszczanski

A Map is an abstract data type (ADT) that models a searchable collection of key-value entries. In a Map, multiple entries with the same key are not allowed. Some applications include:

Another name for a Map is an associative container. The Map ADT is outlined as follows:

If we implement a Map using a list, where each entry in the list is a key-value object then the time complexity of get() and remove() is going to be O$(n)$ since in the worst case we will have to go through the whole list to find the (k, v) pair we are looking for. If the list is sorted by keys then put() will be an O$(n)$ operation since in the worst case we have to do $n$ comparisons. However, if the list is not sorted put() will just be O$(1)$ since we can just put the new (k, v) pair at the end of the list. However, there is a way to implement a Map in which all three of those operations will be O$(1)$. To do this, we need to implement the Map as a direct address table. A direct address table is a Map in which:

Because we can directly access any (k, v) pair by calling A[k], all three operations in this case will be O$(1)$ time. The space complexity will be O$(N)$ since we will need $N$ slots regardless of $n$, where $n$ is the number of entries. If you consider this closely, you will realize that a direct address table is not very efficient unless $n$ and $N$ are close in value. Otherwise, we have a bunch of empty slots just taking up memory. That's where the idea of hash functions comes into play. If we have keys not in the range $[0, N - 1]$ then we need to use a hash function to map the keys to table indices in the address table. In this case, the table becomes a hash table and it consists of:

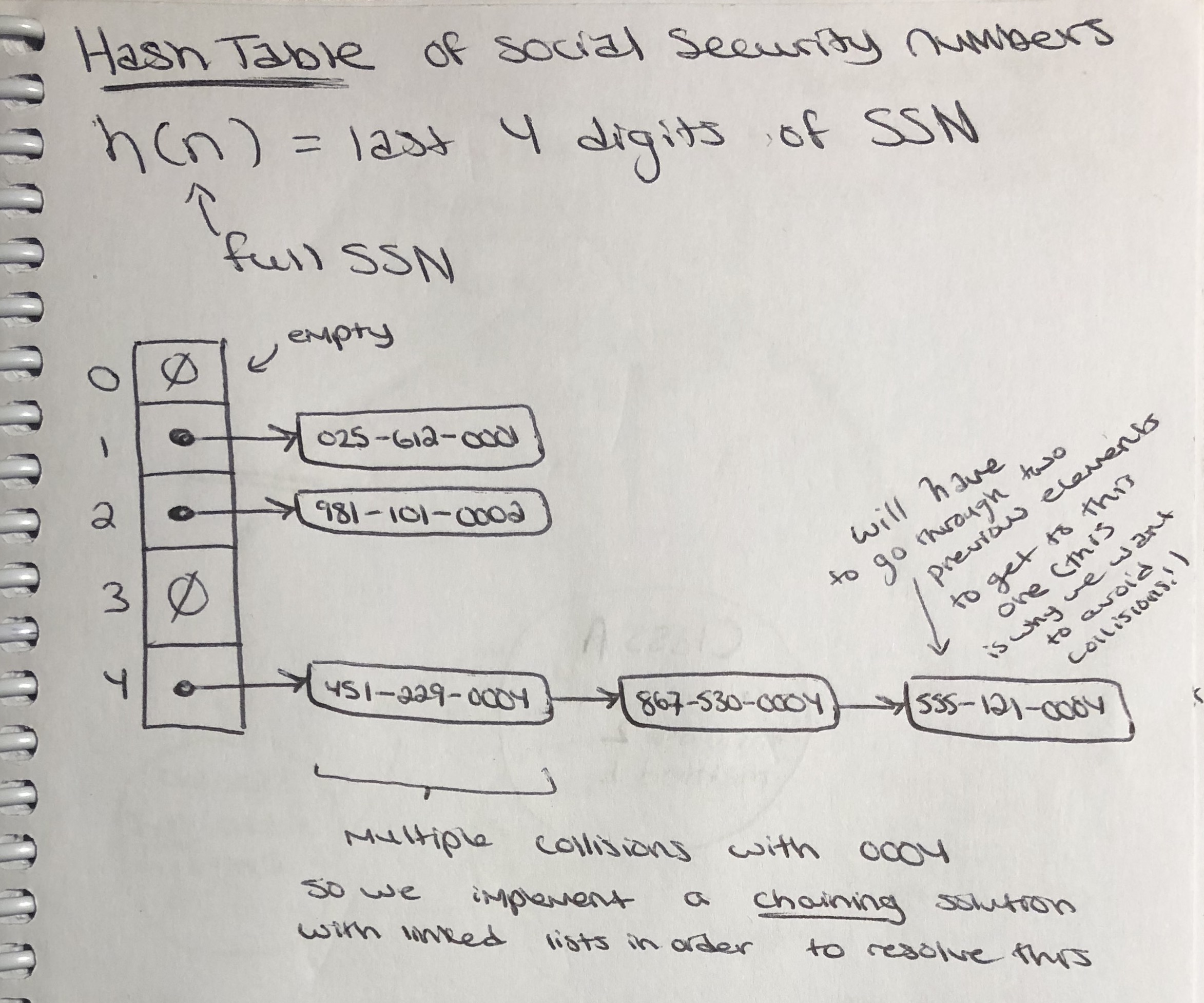
The hash function is a mapping of key $k$ onto an index in $[0, N - 1]$. We can think of it as $h(k) \rightarrow [0, N - 1]$. An example of a hash function would be a modular arithmetic function such as $h(k) = k \text{ mod } N$. The goal of all of this is to store entries (k, v) at indices $i = h(k)$. Now you might ask yourself, what happens if two different (k, v) pairs map to the same index $i$. This is called a collision. There are two common solutions to this problem:

When assessing the performance of a hash table, we often consider something called the load factor $\lambda = \frac{n}{N}$, where $n$ is the number of entries and $N$ is the size of the array. If we pick a hash function $h$ such that the hash values are random, the expected (average) number of probes for an insertion using open addressing will be:

$$\frac{1}{1 - \lambda} = \frac{1}{1 - n/N} = \frac{1}{(N - n)/N} = \frac{N}{N - n}$$

So the expected, or average, runtime of insertion and all other Map ADT operations will be O$(1)$. Note carefully that this is only the average runtime. The worst-case runtime is still going to be O$(n)$ since it is still technically possible to have the maximum number of collisions even with a randomizing hash function. Also note that the closer that $\lambda$ is to 1, the better performance we can expect. If $\frac{n}{N} << 1$ then we are wasting space, and if $\frac{n}{N} >> 1$ we will have too many collisions. The former wastes space, the latter wastes time.

During this semester, we implemented a hash table using a Python dictionary in order to efficiently find if for a given an integer $n$ and list of integers $L$, any integers in $L$ summed to $n$. We then compared our solution to one in which we find possible sums using a double for-loop (O$(n^2)$) to see which was faster. As expected, the hash table was much more efficient as we increased the size of $L$, because on average the hash table could conduct its operations in O$(1)$ time. Here is the code:

from typing import List
from time import perf_counter
import random


# Returns all pairs of integers that sum to number parameter
def two_sum_hash(int_list: List[int], number: int) -> List[List[int]]:
    sums = []
    hash_table = {}

    # We check each integer in the list
    for i in range(len(int_list)):
        # We want to see if the number parameter minus the current number in the list is also in the list
        sum_minus_element = number - int_list[i]

        # Check if sum_minus_element is already in the hash_table
        if str(sum_minus_element) in hash_table:
            # If sum_minus_element is in the hash table, then element + sum_minus_element is a valid sum
            sums.append([int_list[i], sum_minus_element])

        # Add current element to the hash table
        hash_table[str(int_list[i])] = int_list[i]

    # Returns all integer pairs that sum to number parameter
    return sums


def two_sum_dbl_loop(int_list: List[int], number: int) -> List[List[int]]:
    sums = []

    for i in range(len(int_list)):
        for j in range(i + 1, len(int_list)):
            # print(str(i) + ' ' + str(j))
            if int_list[i] + int_list[j] == number:
                sums.append([int_list[i], int_list[j]])

    return sums

and here is the test of the code:

def main():
    int_list = random.sample(range(1, 100000), 10000)
    sum_int = input("Enter an integer ('q' to quit): ")
    while sum_int.lower() != 'q':
        try:
            print("Hash Method:")
            sum_int = int(sum_int)
            start = perf_counter()
            sums = two_sum_hash(int_list, sum_int)
            end = perf_counter()
            hash_time = end - start
            print(f"Pairings that sum to {sum_int}:")
            if sums != []:
                for i in range(len(sums)):
                    print(f"{sums[i][0]} + {sums[i][1]} = {sum_int}")
            else:
                print("None")
            print(f"Time taken to find pairings: {round(hash_time, 6)} seconds")
            print()

            print("Double Loop Method:")
            start = perf_counter()
            sums = two_sum_dbl_loop(int_list, sum_int)
            end = perf_counter()
            dbl_loop_time = end - start
            print(f"Pairings that sum to {sum_int}:")
            if sums != []:
                for i in range(len(sums)):
                    print(f"{sums[i][0]} + {sums[i][1]} = {sum_int}")
            else:
                print("None")
            print(f"Time taken to find pairings: {round(dbl_loop_time, 6)} seconds")

        except:
            print("Error. Invalid parameter passed to two_sum() function.")

        sum_int = input("Enter an integer ('q' to quit): ")


if __name__ == '__main__':
    main()

which might give an output something like this:

Enter an integer ('q' to quit): 45
Hash Method:
Pairings that sum to 45:
None
Time taken to find pairings: 0.011054 seconds

Double Loop Method:
Pairings that sum to 45:
None
Time taken to find pairings: 6.138272 seconds
Enter an integer ('q' to quit): 432
Hash Method:
Pairings that sum to 432:
399 + 33 = 432
284 + 148 = 432
Time taken to find pairings: 0.013764 seconds

Double Loop Method:
Pairings that sum to 432:
148 + 284 = 432
33 + 399 = 432
Time taken to find pairings: 6.281737 seconds
Enter an integer ('q' to quit): q

Some other applications of hash tables caches. A cache is an auxiliary data table with limited space that is used to speed up access to data that is primarily stored in slower media. In most implementations, hash collisions are handled by discarding the older of the two colliding entries. This ensures every item in the table has a unique hash value, and also means that the data in the cache will be data the has been used more recently. The fact that each item in the table will have a unique hash value ensures that the table will be operating as efficiently as possible, provided that $\lambda \approx 1$, which is generally the case with caches.

Hash Zine
Hash Zine